Pengenalan Struktur Data

Pengenalan Struktur Data 

Struktur data adalah cara menyimpan atau merepresentasikan data di dalam komputer agar bisa dipakai secara efisien Sedangkan data adalah representasi dari fakta dunia nyata. 

Fakta atau keterangan tentang kenyataan yang disimpan, direkam atau direpresentasikan dalam bentuk tulisan, suara, gambar, sinyal atau simbol.

Secara garis besar type data dapat dikategorikan menjadi :

1. Type data sederhana, meliputi :

a. Type data sederhana tunggal, misalnya

  Integer, real, boolean dan karakter

b. Type data sederhana majemuk, misalnya

         String

2. Struktur Data, meliputi :

a. Struktur data sederhana, misalnya array dan record

b. Struktur data majemuk, yang terdiri dari

Linier : Stack, Queue, serta List dan Multilist

Non Linier : Pohon Biner dan Graph

Pemakaian struktur data yang tepat di dalam proses pemrograman akan menghasilkan algoritma yang lebih jelas dan tepat, sehingga menjadikan program secara keseluruhan lebih efisien dan sederhana.

Tipe-tipe Data

Secara sederhana tipe data dapat didefinisikan dengan istilah tempat untuk menentukan pemberian nilai terhadap suatu variabel sesuai atau tidak dengan nilai yang diberikan oleh user. Dalam versi lain tipe data juga diartikan sebagai batasan terhadap fungsi tanda pengenal terhadap semua nilai yang diterima. logika yang dapat kita berikan adalah ketika kita menempatkan tanda pengenal harga hanya mengenal angka, maka ketika kita memberikan nilai berupa string maka secara otomatis data tersebut akan ditolak karena nilai tersebut tidak dikenali oleh tipe data yang diberikan.

 
1. Tipe Data Numeric Integer

Tipe data integer merupakan tipe data bilangan bulat yang hanya mengenal bilangan decimal. Dimana tipe data Integer tidak mengenal pecahan

Bentuk Umum

Var
Nil1:integer;
Begin
Nil1:=5000;

2. Tipe Data Real

Tipe data numeric real adalah tipe data dari suatu tanda pengenal selain mengenal bilangan bulat utuh tipe data ini juga mengenal nilai angka yang mengenal pecahan.

Bentuk Umum

Var
Nil:real;
Begin
Nil1:=20,5;

3. Tipe Data String
Tipe data string merupakan salah satu jens tipe data selain mengenal angak disini tipe data dapat juga mengenla data berupa huruf maupun tanda baca.

Bentuk umum

Var
Nama:string;
Begin
Nama:=’Anton’;

4. Tipe Data Char

Secara fungsi tipe data char sama dengan tipe data string tetapi dari segi kapsitas ruang diperoleh tipe data char jauh lebih sedikit karena hanya mengenal 1 karakter.

Struktur data yang ″standar″ yang biasanya digunakan dibidang informatika adalah :

• ·          List linier (Linked List) dan variasinya Multilist
• ·          Stack (Tumpukan)
• ·         Queue (Antrian)
• ·          Tree ( Pohon )
• ·          Graph ( Graf )

RECORD (REKAMAN)

Disusun oleh satu atau lebih field. Tiap field menyimpan data dari tipe dasar tertentu atau dari tipe bentukan lain yang sudah didefinisikan sebelumnya. Nama rekaman ditentukan oleh pemrogram.

Rekaman disebut juga tipe terstruktur.

Contoh :

1. type Titik : record

jika P dideklarasikan sebagai Titik maka

mengacu field pada P adalah P.x dan P.y.

2. Didefinisikan tipe terstruktur yang mewakili Jam yang terdiri

atas jam (hh), menit (mm) dan detik (ss), maka cara menulis

type Jam adalah :

type JAM : record

mm : integer, {0…59}

ss : integer {0…59}>

Jika J adalah peubah (variabel) bertipe Jam

maka cara mengacu tiap field adalah J.hh, J.mm dan J.ss

 

IMPLEMENTASI STRUKTUR DATA DALAM LINGKUP ARRAY, LINKED-LIST, DAN ANTRIAN

Pada pemrograman prosedural, setiap data mempunyai jenis. Jenis data menentukan bagaimana mengartikan nilai dari suatu data serta operasi apa yang dapat dilakukan terhadap data tersebut.

Secara umum jenis data dapat digolongkan menjadi 4 golongan, yaitu :

1. jenis dasar, adalah jenis data yang dianggap sudah terdefinisi misalnya integer, real, boolean, character; suatu data yang memiliki jenis ini setiap saat hanya dapat memiliki satu nilai. 

2. jenis bentukan, adalah jenis data yang merupakan komposisi dari jenis dasar; suatu data yang memiliki jenis ini setiap saat hanya dapat memiliki satu nilai yang sesuai dengan susunan dari jenis dasar yang didefinisikannya. 

3. tabel, adalah jenis data yang terdiri atas sekumpulan unsur berjenis sama yang tersusun secara kontinu dan setiap unsur dapat diperoleh melalui indeks tabel; suatu data yang memiliki jenis ini setiap saat dapatmemiliki banyak nilai sesuai dengan ukuran tabel. 

4. pointer, adalah jenis data yang menyimpan alamat komputer dari suatu data.
Data yang ada di dunia nyata seringkali amat kompleks, sehingga membutuhkan suatu abstraksi dari representasi data tersebut, agar memudahkan dalam merancang struktur datanya. 

Dikenal 3 tingkatan abstraksi yaitu:

1. definisi fungsional

    
Dilakukan pendefinisian suatu struktur data dan operator-perator yang berlaku pada struktur tersebut. Untuk melakukannya tidak digunakan notasi khusus melainkan mendefinisikan dengan kata-kata.

2. representasi logika

Representasi logika adalah rincian jenis dari struktur data, menyangkut nama jenis dan jenis-jenis operator. Untuk membuat representasi lojik digunakan notasi algoritmik. Representasi ini tak bergantung pada memory komputer.

Pada representasi logika belum digunakan jenis data yang sudah dikenal di atas. Relasi antara definisi fungsional dan representasi logika adalah satu-ke-satu, artinya setiap definisi fungsional hanya mempunyai satu representasi logika. 

3. representasi fisik

Representasi fisik adalah spesifikasi dari struktur data sesuai dengan implementasinya pada memory komputer. Digunakan notasi algoritma dan type-type dasar yang sudah dikenal. Pada dasarnya hanya ada dua macam representasi fisik yaitu: kontigu dan berkait. Untuk satu representasi logika bisa dikembangkan menjadi banyak kemungkinan representasi fisik.

A. ARRAY

1.      Array suatu dimensi

Array suatu dimensi tidak lain adalah kumpulan elemen-elemen yang identik, yang tersusun dalam satu baris. Elemen-elemen tersebuit memiliki type data yang sama, tetapi isi dari elemen tersebut boleh berbeda-beda.

Pendeklarasian array diawali denga kata baku type dan diikuti dengan nama array dan tanda samaq dengan (=), lalu kata baku array beserta range indeks dan diakhiri dengan kata baku of beserta type datanya.

Bentuk umum dari deklarasi tipe array adalah :

type pengenal = array [tipe_index] of tipe;
dengan pengenal : nama tipe data
tipe_index : tipe data untuk nomor index
tipe : tipe data komponen

Parameter tipe_index menentukan banyaknya komponen array tersebut. Parameter ini boleh berupa sembarang tipe ordinal kecuali logint dan sub jangkauan dari logint. 

Berikut contoh dari deklarasi :
type vek = array [1…..100] of integer;
menunjukkan bahwa vek adalah tipe data yang berupa array yang komponennya bertipe integer dan banyaknya 100 buah.
Deklarasi yang demikian ini disebut deklarasi array dimensi satu, yang kami sebut vektor. 

2.      Array dua dimensi

Array dua dimensi, yang sering digambarkan pada sebuah matrix adalah merupakan sebuah perluasan dari sebuah array satu dimensi. Jika pada array satu dimensi hanya terdiri dari sebuah baris dengan beberapa kolom elemen maka pada array dua dimensi terdiri dari beberapa baris dan beberapa kolom elemen yang bertype sama. Jika tipe komponen juga berupa larik lain, akan kita peroleh array demensi banyak.

 Sebagai contoh :
type Pkl = array [1…..100] of array [1…….5] of real;

menunjukkan bahwa Pkl adalah vektor yang terdiri dari 100 komponen, dengan tipe komponennya adalah sebuah vektor lain yang mempunyai 5 komponen bertipe real. Bentuk ini sering disebut dengan deklarasi array dimensi dua yang kami sebut sebagai tabel atau matrix.

3.      Array tiga dimensi

Array tiga dimensi dapat digambarkan sebagai suatu benda ruang. Deklarasi pada array tiga dimensi tidak berbeda pada array satu dimensi dan dua dimensi yang telah dijelaskan sebelumnya, kecuali pada indeks array.

type Pkl = array [1…..100,1……5] of real;

contoh lain misalnya :
type Katro = array [boolean,1…..100,1……5] of char;
deklarasi diatas disebut sebagai deklarasi array dimensi tiga. 

4.  Array banyak dimensi

Sebenarnya array banyak dimensi tidak terlalu sering dipakai seperti halnya array satu dimensi, dua dimensi, dan tiga dimensi. Namun hal itu bukan berarti pascal tidak membolehkan anda memakainya. Array banyak dimensi ini pada dasarnya sama dengan array sebelumnya kecuali pada jumlah dimensinya saja.

 

B. Linked List 

  Linked list atau senatai berantai adalah kunpulan liniar sejumlah data , atau kumpulan komponen yang disusun secara berurutan pointer. Masing-masing komponen dinamakan dengan simpul (node). Simpul dalam suatu Linked list terbagi menjadi dua bagian yaitu medan informasi yang berisi informasi yang akan disimpan dan diolah, dan medan penyambung (Link field) yang berisi simpul berikutnya.

Ada sejumlah operasi yang bisa kita lakukan pada sebuah Linked list yaitu membaca isi link, menambah simpul, menghapus simpul dan mencari informasi pada Linked list . 

1. Menambah simpul 

Operasi menambah simpul bisa dipecah berdasarkan posisi simpul dabu yang akan di sisipkan, yaitu simpul baru selalu diletakkan sebagai simpul pertama, dan simpul baru menyisip diantara kedua simpul yang sudah ada.

Berikut contohnya : 

type Simpul = ^Data ;
Data = record
Info : char ;
Berikut : Simpul ;
end ;
var Element : char ;
Awal, Akhir, Baru : Simpul ;

2. Menambah di Belakang 

Operasi penambahan simpul pada Linked list adalah penambahan suatu Linked list. Simpul-simpul abru yang ditambahkan selalu menjadi simpul terakhir. 

 Prosedur yang bisa dipanggil dengan memanggil prosedur :
TAMBAH_BELAKANG (Awal, Akhir, Elemen);

Program selengkapnya adalah : 

procedure TAMBAH_BELAKANG (var Awal, Akhir : Simpul ;
Elemen : char ) ;
var Baru : Simpul ;
begin
new (Baru) ; Baru^.Info :=Elemen;
if Awal = nil then
Awal := Baru
else
Akhir^.Berikut := Baru;
Akhir := Baru;
Akhir^.Berikut := nil
end ;

3. Menambah didepan 

Operasi penambahan simpul baru akan selalu diletakkan diawal link. Prosedur untuk menambah simpul bisa dipanggil dengan menggunakan : 

TAMBAH_DEPAN (Awal, Akhir, Elemen);

Program selengkapnya adalah : 

procedure TAMBAH_DEPAN (var Awal, Akhir : Simpul ;
Elemen : char ) ;
var Baru : Simpul ;
begin
new (Baru) ; Baru^.Info :=Elemen;
if Awal = nil then
Akhir := Baru
else
Baru^.Berikut := Awal;
Awal := Baru;
end ;

4. menambah ditengah 

Untuk menembah ditengan linked list memerlukan memerlukan bantuan pointer misalnya bantu, perhatikan contoh program berikut ;
procedure TAMBAH_TENGAH(var Awal, Akhir : Simpul ;
Elemen : char ) ;
var Baru, Bantu : Simpul ;
begin
new (Baru) ; Baru^.Info :=Elemen;
if Awal = nil then
begin
Awal := Baru;
Akhir := Baru;
end;
else
begin
Bantu := Awal;
while Elemen > Baru^.Berikut^.Info do
Bantu := Bantu^.Berikut;

Baru^.Berikut := Bantu^.Berikut;
Bantu^.Berikut := Baru;
end;
end ;

5. Menghapus Simpul 

Operasi kedua yang akan dijelaskan adalah operasi menghapus simpul. Dalam menghapus simpul ada suatu hal yang perlu diperhatikan, yaitu bahwa simpul yang bias dihapus adalah simpul yang berada sesudah simpul yang ditunjukan oleh suatu pointer, kecuali untuk simpul pertama. Dengan demikian kita tidak bias menghapus simpul yang ditunjuk oleh suatu pointer atau simpul sebelumnya.

6. Menghapus simpul pertama 

Untuk menghapus simpul pertama, maka pointer bantu kita dibuat sama dengan pointer awal. Kemudian pointer awal kita pindah kesimpul yang ditunjuk oleh pointer pada simpul yang ditunjuk oleh pointer Bantu. Selanjutnya, simpul yng ditunjuk oleh pointer Bantu kita dispose.

7. Menghapus simpul ditengah atau terakhir. 

Untuk menghapus simpul yang berada di tengah senarai berantai, pertama kali kita letakan pointer Bantu pada simpul di sebelah kiri simpul yang akan dihapus. Simpul yang akan dihapus kita tunjuk dengan pointer lain. Kemudian, pointer pada simpul yang ditunjuk oleh Bantu kita tunjukan pada simpul yang ditunju oleh pointer pada simpul yang akan dihapus. Selanjutnya simpul yang ditunjuk oleh pointer hapus kita dispose.

8. Senarai berantai berkepala 

Suatu saat kita perlu meletakan sebuah simpul sebagai simpul pertama dari sebuah senarai berantai untuk maksud-maksud tertentu. Simpul ini tidak berisi informasi seperti halnya simpul-simpul lain dalam senarai berantai, tapi keberadaannya sangat diperlukanuntuk lebih mempercepat proses eksekusi. Simpul yang demikian disebut dengan simpul kepala (Header Lode) sehingga senarai berantai disebut senarai berantai berkepala (Headed Linked-List)

9. Senarai berantai sebagai tumpukan. 

Operasi penambahan simpul baru diawal suatu senarai berantai, sehingga simpul baru adalah sebagai simpul pertama (harap dibedakan antara simpul kepala dan simpul pertama), serupa dengan operasi mempush (memasukan elemen kedalam suatu tumpukan. Dalam kedua kasus ini, elemen baru yang ditambahkan adalah satu-satunya elemen dalam kumpulan elemen yang bisa segera dimasuk. Tumpukan hanya bisa dimasuk lewat elemen pertama yang menempati posisi teratas dalam tumpukan, dan senarai berantai hanya bisa dimasuk lewat pointer yang menuju ke elemen pertama. Demikian juga halnya dengan operasi POP (menghapus elemen dari suatu tumpukan). Dalam kedua kasus ini hanya elemen pertama yang bisa dimasuk (dihapus), dan elemen berikutnya menjasi elemen baru yang bisa segera dimasuk setelah elemen sebelumnya di POP.
Dengan demikian kita bisa menyejikan tumpukan dengan cara lain, yaitu dengan senarai berantai linear. Elemen pertama dalam senarai berantai diperlakukan sebagai elemen teratas dari tumpukan. Dengan mengacu pada prosedur PUSH dan POP kita bisa menyusun prosedur PUSH dan POP yang baru dengan mengingat bahwa kita ingin menyajikan tumpukan menggunakan senarai berantai.

10. Single linked list 

Apabila setiap kali anda ingin menambahkan data selalu dengan menggunakan variabel pointer yang baru, anda akan membutuhkan banyak sekali variabel pointer (penunjuk). Jika anda hanya menggunakan satu variabel pointer saja untuk menyimpan banyak data dengan metoda yang kita sebut linked list. Jika diterjemahkan, maka berarti suatu daftar isi yang saling berhubungan.

Dalam pembuatan single linked list dapat menggunakan dua metoda: 

a. LIFO (Last In First Out) aplikasinya : Stack (Tumpukan)
Adalah suatu metoda pembuatan linked list dimana data yang masuk paling akhir adalah data yang keluar paling awal. 

b. FIFO (First In First Out) aplikasinya : Queue (Antrian)
Adala suatu metoda pembuatan linked list dimana data yang masuk paling awal adalah data yang keluar paling awal juga.

C. QUEUE (ANTRIAN)
Antrian adalah suatu kumpulan data yang mana penambahan elemenhanya bisa dilakukan pada suatu ujung (disebut dengan sisi belakang/ real), dan penghapusan (pengambilan elemen) dilakukan lewat ujung lain (disebut dengan sisi depan/ front). 

Seperti yang kita ketahui, tumpukan menggunakan prinsip masuk terakhir keluar pertama atau LIFO (Last In First Out), maka pada antrian prinsip yang digunakan adalah masuk pertama keluar pertama atau FIFO (First In First Out). Dengan kata lain, urutan keluaran elemen akan sama dengan urutan masuknya.

Queue jika diartikan secaara harfiah berarti antrian. Queue merupakan salah satu contoh aplikasi dari pembuatan double linked-list yang cukup sering kita temuai dalam kehidupan sehari-haAntrian sebenarnya juga merupakan satu kumpulan data, tipe data yang sesuai untuk menyajikan antrian adalah menggunakan larik dan senarai berantai. untuk menyajikan antrian menggunakan larik, maka kita membutuhkan deklarasi antrian, misalnya sebagai berikut : 

Const Max_Elemen = 100;
Type Antri = array [1.. Max_Elemen] of integer;
Var Antrian : Antri;
Depan,
Belakang : integer; 

Dalam deklarasi di atas, elemen antrian dinyatakan dalam type integer. Perubahan depan menunjukan posisi elemenpertama dalam larik; perubahan belakang menunjukan posisi elemen terakhir dalam larik. 

TREE DAN BINARY TREE 

 

A. TREE
Adalah Kumpulan elemen yang salah satu elemennya disebut dengan root (akar) dan sisa elemen yang lain disebut sebagai simpul (node/vertex) yang terpecah menjadi sejumlah himpunan yang tidak saling berhubungan satu sama lain, yang disebut subtree/cabang.

B. BINARY TREE
Dalam ilmu computer, sebuah pohon biner (binary tree) adalah sebuah pohon struktur data dimana setiap simpul memiliki paling banyak dua anak. Secara khusus anaknya dinamakan kiri dan kanan, penggunaan secara umum pohon biner adalah Pohon biner terurut, yang lainnya adalah heap biner.

Dalam pohon biner terurut memiliki sifat-sifat sebagai berikut:

 Karakteristik pohon biner yaitu: 

• Setiap simpul paling banyak hanya mempunyai dua buah anak 
• Derajat tertinggi dari simpul dalam pohon biner adalah dua 
• Banyaknya simpul maksimum pada tingkat 2^n.
• Dalam pohon biner dimungkinkan tidak mempunyai simpul.

Dalam struktur biner induk simpul hanya dapat memiliki 2 anak simpul (sub pohon kiri dan sub pohon kanan) dan maksimum jumlah node pada setiap tingkat  adalah 2 pangkat n ()

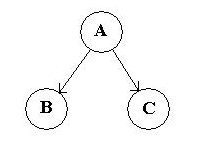
Ket:
A          : Induk Simpul
B          : Anak Simpul/sub pohon kiri (nilai lebih kebil dari nilai induk)
C          : Anak simpul/sub pohon kanan (nilai lebih besar dari nilai induk)

Create Tree (P)                 = Membuat pohon biner baru.
Empty Tree (P)                 = Memeriksa apakah biner kosong.
Insert Tree (P,N)               = Menyisipkan simpul baru..
Delete Tree (P,N)              = Menghapus simpul.
Info (P)                             = Mengetahui atau mencetak isi simpul P.
Traversal                          = Penulusuran pohon biner.
P                                       = Pohon
N                                      = Nilai masukan

Contoh :